Twenty-second meeting: Saturday, April 8, 2023

Location: SAS 1102, North Carolina State University, Raleigh

Parking: Local parking on SAS is free during the event

Speakers:
Ed Allen (Wake Forest University, US), Nantel Bergeron (York University, Canada), Carly Klivans (Brown University, US), and Bruce Sagan (Michigan State University, US).

Tentative Conference Schedule (all times in EST)
(Abstracts can be found below)

09:00 – 10:00am, welcome
10:00 – 11:00am, Nantel Bergeron
11:00 – 11:30am, coffee break
11:30 – 12:30pm, Caroline Klivans
12:30 – 2:30pm, lunch break
02:30 – 3:30pm, Edward Allen
03:30 – 4:00pm, coffee break
04:00 – 5:00pm, Bruce Sagan

Registration:
To register, please fill out this form.

Lunch break: 
There are many restaurants and take-out places around campus. In particular, in Hillsborough street you can find Bul-box, Lemon & lime, Guasaca, Chipotle, Jasmin & Olive, Player’s retreat, David’s dumplings, among others. Also in the Cameron Village, which is ~15 minutes walking-distance, you can find other places like CAVA, Cantina 18, Kale me crazy, and many more.

Organizing Committee: Laura Colmenarejo (NCSU), Sarah K. Mason (Wake Forest University), Nick Mayers (NCSU), and Clifford Smyth (UNC Greensboro)

Titles and Abstracts

Ed Allen: Tunnel hook fillings and a combinatorial interpretation of the noncommutative inverse Kostka matrix

The inverse Kostka matrix is the transition matrix between the Schur functions and the complete homogeneous symmetric functions. Eğecioğlu and Remmel developed a combinatorial interpretation for the entries of this matrix using special rim hooks to decompose Ferrers partition diagrams. Recently, Berg, Bergeron, Saliola, Serrano, and Zabrocki introduced the immaculate basis in the space of noncommutative symmetric functions (NSYM) which are an analogue of Schur functions. We generalize Eğecioğlu’s and Remmel’s special rim hooks by introducing new diagrams for skews of integer sequences (involving colored cells) and filling the diagrams with objects we call tunnel hook fillings. This method also gives a combinatorial interpretation to the expansion of monomial quasisymmetric functions into dual immaculates. Finally, we show how tunnel hook fillings can be used to extend Campbell’s results on ribbon decompositions of immaculate functions to a larger class of shapes.

Nantel Bergeron: The excedance quotient of the Bruhat order, Quasisymmetric Varieties and Temperley-Lieb algebras

Let 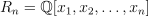be the ring of polynomial in n variables over the rationals and consider the ideal 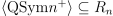generated by quasisymmetric polynomials without constant term. It was shown by J. C. Aval, F. Bergeron and N. Bergeron that 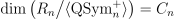, the n-th Catalan number. In the present work, we explain this phenomenon by defining a set of permutations with the following properties: first, 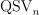is a basis of the Temperley–Lieb algebra 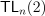, and second, when considering 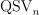as a collection of points in 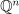, the top-degree homogeneous component of the vanishing ideal 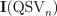is 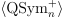. Our construction has a few byproducts which are independently noteworthy. We define an equivalence relation on the symmetric group 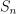using weak excedances and show that its equivalence classes are naturally indexed by noncrossing partitions. Each equivalence class is an interval in the Bruhat order between an element of 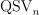and a 321-avoiding permutation. Furthermore, the Bruhat order induces a well-defined order on 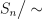. Finally, we show that any section of the quotient 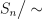gives an (often novel) basis for .
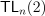This is joint work with L. Gagnon.

Carly Klivans: The Mathematics of Chip-Firing

Chip-firing processes are discrete dynamical systems. A commodity (chips, sand, dollars) is exchanged between sites of a network according to simple local rules. Although governed by local rules, the long-term global behavior of the system reveals unexpected properties, including intricate fractal-like patterns. Early results related chip-firing to classic combinatorial objects such as spanning trees, parking functions, and matroids. In recent years, chip-firing has seen much activity in new directions. Connections have been made, for example, between chip-firing and Coxeter groups, binomial ideals, and Riemann surfaces. In this talk, I will give a broad survey of the theory of chip-firing and its many ties to algebraic combinatorics.

Bruce Sagan: Stirling numbers for complex reflection groups

The ordinary Stirling numbers count set partitions and permutations of
{1, 2, . . . , n} by number of subsets and number of cycles, respectively. We show how to generalize these concepts to a complex reflection group. The ordinary Stirling numbers are recovered in type A. It turns out that often these Stirling numbers can be expressed in terms of elementary and homogeneous symmetric functions. We also make a connection with super coinvariant algebras. All terminology concerning Stirling numbers, symmetric functions, and complex reflection groups will be defined. This is joint work with Joshua Swanson.